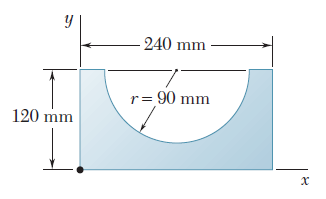
| Determine el momento de inercia del área sombreada con respecto al eje x |
| SOLUCIÓN |
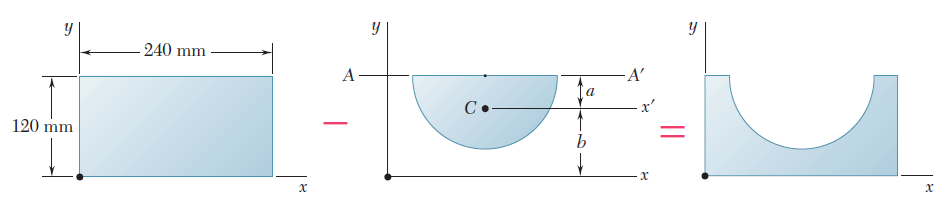
El área dada puede obtenerse restándole un semicírculo a un rectángulo. Los momentos de inercia es rectángulo y del semicírculo serán calculados en forma separada |
|
Momento de inercia de rectángulo. Haciendo referencia a los contenidos antes expuestos, tenemos:
|
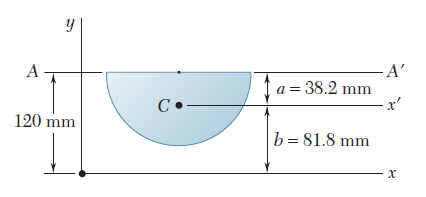
Momento de inercia del semicírculo. Haciendo referencia a la figura para determinar la ubicación del centroide C el semicírculo y respecto al diámetro AA´. |
|
|
La distancia b desde el centroide C hasta el eje x es
Ahora, se calcula el momento de inercia del semicírculo con respecto al diámetro AA´; además, se calcula el área del semicírculo.
Con el teorema de los ejes paralelos se obtiene el valor de '
' '
De nuevo, con el teorema de los ejes paralelos, se obtiene el valor de Ix :
Momento de inercia del área dada. Si se le resta el momento de inercia del semicírculo al momento de inercia es rectángulo, se obtiene
|
