Una avioneta viaja horizontalmente a una altura de 50 metros, con una rapidez de 540 km/h. La avioneta suelta un paquete con provisiones para una persona extraviada en la montaña. Calcule:

1. El tiempo que el paquete tarda en caer
2. La velocidad con la que el paquete impacta con el suelo.
3. La distancia horizontal a la que debe soltarse el paquete, para que caiga junto a la persona extraviada.

Analizando el movimiento vertical:

a) Tiempo en bajar

$y_o=50m$

$y=0$

$v_{oy}=0$

Entonces:

$y=y_o+v_{oy}t-1/2g{t}^2$

$0=y_o+\left(0\right)t-1/2g{t}^2$

$1/2g{t}^2=y_o$

$t^2=\frac{2y_o}{g}$

$t=\sqrt{\frac{2y_o}{g}}$

$t=\sqrt{\frac{2\left(50m\right)}{9.8m/s^2}}$

$t=3.19s$ (tiempo que tarda en bajar)

b) Velocidad de impacto con el suelo:

Componente vertical de la velocidad con la que impacta con el suelo:

$v_y=v_{oy}-gt$

$v_y=0-gt$

$v_y=-(9.8m/s^2)(3.19s)$

$v_y=-31.26m/s$

Analizando el movimiento horizontal:

$x_o=0$

$x=?$

$v_{ox}=\frac{540km}{h}x\frac{1000m}{1km}x\frac{1h}{3600s}=150m/s$

$a_x=0$

Entonces:

$x=x_o+v_{ox}t+1/2a_x{t}^2$

$x=0+(150m/s)t+1/2\left(0\right)t^2$

$x=(150m/s)t$

$x=(150m/s)(3.19s)$

$x=478.5m$

También:

$v_x=v_{ox}+a_{x}t$

$v_x=v_{ox}+\left(0\right)t$

$v_x=150m/s$ (la componente horizontal de la velocidad no cambia)

$Entonces:$

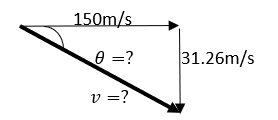
Utilizando la fórmula para encontrar la magnitud del vector de velocidad:

$v=\sqrt{{v_x}^2+{v_x}^2}$

$v=\sqrt{{(150m/s)}^2+{(31.26m/s)}^2}$

$v=153.22m/s$

Y el ángulo del vector de velocidad con la horizontal:

$\theta ={\tan }^{-1}\left|\frac{v_y}{v_x}\right|$

$\theta ={\tan }^{-1}\left|\frac{31.26}{150}\right|$

$\theta =11.77°$

c) la distancia horizontal que recorre ya la calculamos en el literal anterior:

$x=478.5m$

Presentación en Power Point paso a paso (opcional)   Click aquí