Una pelota se lanza con una rapidez inicial de 60 p/s y un ángulo de inclinación respecto a la horizontal. La pelota impacta justo en el punto mostrado. Encuentre el ángulo de tiro.

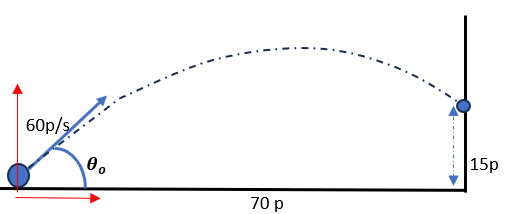
Analizando en y:

$y_o=0$

$y=15p$

$v_{oy}=v_{o}sen{\theta }_o=(60p/s)sen{\theta }_o$

Entonces:

$y=y_o+v_{oy}t-1/2g{t}^2$

$15p=0+(60p/s)\left(sen{\theta }_o\right)t-1/2(32.2p/s^2)t^2$

$15p=(60p/s)\left(sen{\theta }_o\right)t-(16.1p/s^2)t^2$

$(16.1p/s^2)t^2-(60p/s)\left(sen{\theta }_o\right)t+15p=0$ (ecuación 1)

También analizando en x:

$x_o=0$

$x=70p$

$v_{ox}=v_{o}cos{\theta }_o=(60p/s)cos{\theta }_o$

$a_x=0$

$x=x_o+v_{ox}t+1/2a_x{t}^2$

$70p=0+(60p/s)cos{\theta }_{o}t+1/2\left(0\right)t^2$

$70p=(60p/s)cos{\theta }_{o}t$

$\frac{70p}{(60p/s)cos{\theta }_o}=t$

(ecuación 2)

Sustituyendo la ecuación 2 en la ecuación 1:

$(16.1p/s^2)t^2-(60p/s)\left(sen{\theta }_o\right)t+15p=0$

$(16.1p/s^2)(\frac{70p}{(60p/s)cos{\theta }_o}{)}^2-(60p/s\left)\right(sen{\theta }_o\left)\right(\frac{70p}{(60p/s)cos{\theta }_o})+15p=0$

$\frac{21.91}{{\cos }^2{\theta }_o}-70tan{\theta }_o+15=0$

$21.91se{c}^2{\theta }_o-70tan{\theta }_o+15=0$

$21.91(1+{\tan }^2{\theta }_o)-70tan{\theta }_o+15=0$

$21.91+21.91{\tan }^2{\theta }_o-70tan{\theta }_o+15=0$

$21.91{\tan }^2{\theta }_o-70tan{\theta }_o+36.91=0$

Aplicando la fórmula general:

$tan{\theta }_o=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$tan{\theta }_o=\frac{-(-70)\pm \sqrt{{(-70)}^2-4(21.91)(36.91)}}{2(21.91)}$

$tan{\theta }_o=\frac{70\pm 40.81}{43.82}$

$tan{\theta }_o=\frac{70+40.81}{43.82}$

$tan{\theta }_o=2.528754$

${\theta }_o={\tan }^{-1}(2.528754)$

${\theta }_o=68.42°$

$tan{\theta }_o=\frac{70-40.81}{43.82}$

$tan{\theta }_o=0.666134$

${\theta }_o={\tan }^{-1}(0.666134)$

${\theta }_o=33.67°$

Por lo tanto hay dos casos en los que ocurre: cuando se lanza a 33.67° y a 68.42°. En cada caso el tiempo es 1.40 s y 3.17 s respectivamente.

Presentación en Power Point paso a paso (opcional)   Click aquí