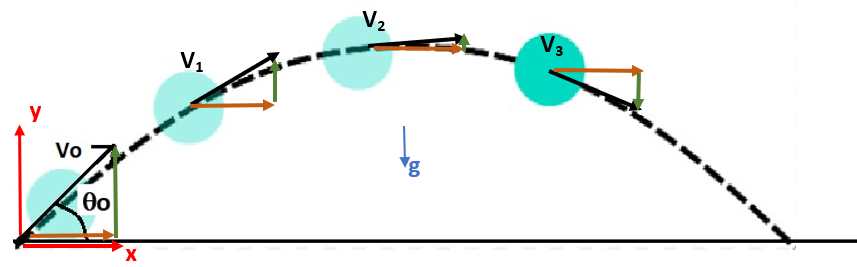
Cuando un objeto es lanzado en un campo gravitatorio (por ejemplo en la tierra, bajo la acción de la gravedad), describe una trayectoria que coincide con una "parábola". El lanzamiento se hace con una velocidad inicial y un ángulo de tiro. Esa velocidad va cambiando de magnitud y dirección, a medida que se mueve en el aire; cuando va hacia arriba su velocidad va disminuyendo y el ángulo que forma esa velocidad con una línea horizontal va disminuyendo, hasta que en el punto de su altura máxima su velocidad es estrictamente horizontal y el ángulo de la velocidad con la horizontal es cero. Cuando va hacia abajo nuevamente la velocidad va aumentando y el ángulo de esa velocidad con la horizontal, va aumentando. |
|
Vamos a decir que es un movimiento en dos dimensiones, debido a que:
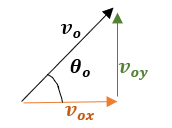
Analizando la velocidad inicial: |
|
Entonces, en base a las razones trigonométricas en un triángulo rectángulo: También: Analizando el movimiento vertical, desde el punto del lanzamiento hasta el punto de su altura máxima:
Como sabemos que el tiempo en subir es igual al tiempo en bajar, entonces el tiempo total de vuelo del objeto es: |
Calculando la altura máxima: Analizando ahora el movimiento horizontal: Entonces: Pero la aceleración es totalmente vertical (g), por lo tanto, la aceleración en x es cero. Considerando el tiempo total de vuelo: pero: Entonces: Concluyendo: las ecuaciones del tiempo total de vuelo, altura máxima alcanzada y alcance, para el movimiento parabólico son: |
Presentación en Power Point paso a paso (opcional) |
Explicación en video (opcional) |
Ejemplo 8.1 |
Ejemplo 8.2 |
Ejemplo 8.3 |
| G. 01 | |



 Click aquí
Click aquí
 Click aquí
Click aquí